5.2.7.2 Filter berechnen
Die Funktionen „lowpass“, „highpass“, „bandpass“ und „bandstop“ berechnen eine Filterung eines Signals mit einem digitalen IIR-Filter. Damit können bestimmte Frequenzanteile eines Signal abgeschwächt werden.
Die Funktion „lowpass“ (Tiefpass) lässt Frequenzanteile unterhalb der eingestellten Grenzfrequenz (Durchlassbereich) ohne oder mit nur geringer Abschwächung (Dämpfung) passieren und schwächt Frequenzanteile oberhalb der eingestellten Grenzfrequenz (Sperrbereich) ab. Die Abschwächung nimmt dabei zu hohen Frequenzen hin zu.
Umgekehrt lässt die Funktion „highpass“ (Hochpass) Frequenzanteile oberhalb der eingestellten Grenzfrequenz (Durchlassbereich) ohne oder mit nur geringer Abschwächung (Dämpfung) passieren und schwächt Frequenzanteile unterhalb der eingestellten Grenzfrequenz (Sperrbereich) ab. Die Abschwächung nimmt dabei zu niedrigen Frequenzen hin zu.
Die Funktion „bandpass“ lässt Frequenzanteile innerhalb der eingestellten Grenzfrequenzen (Durchlassbereich) ohne oder mit nur geringer Abschwächung (Dämpfung) passieren und schwächt Frequenzanteile außerhalb der eingestellten Grenzfrequenzen (Sperrbereich) ab.
Umgekehrt lässt die Funktion „bandstop“ Frequenzanteile außerhalb der eingestellten Grenzfrequenzen (Durchlassbereich) ohne oder mit nur geringer Abschwächung (Dämpfung) passieren und schwächt Frequenzanteile innerhalb der eingestellten Grenzfrequenzen (Sperrbereich) ab.
Die Grenzfrequenzen können im Bereich von 0 Hz bis zur Nyquist-Frequenz eingestellt werden. Die Nyquist-Frequenz entspricht der halben Abtastrate. Dabei sollte ein kleiner Abstand zu 0 Hz und zur Nyquist-Frequenz eingehalten werden, damit die Filter gut funktionieren.
Für „bandpass“ und „bandstop“ muss die untere Grenzfrequenz niedriger als die obere Grenzfrequenz sein.
Weiterhin kann die Filter-Ordnung im Bereich von 1 bis 10 eingestellt werden. Generell nimmt die Dämpfung im Sperrbereich jenseits der Grenzfrequenz für Filter mit höherer Ordnung schneller zu. Filter mit höherer Ordnung benötigen allerdings mehr Rechenleistung.
Optional kann auch die Charakteristik des Filters eingestellt werden. Dabei stehen als Charakteristiken „Butterworth“, „Bessel“ und „Chebyshev“ (deutsch: „Tschebyscheff“) zur Verfügung. Wird keine Charakteristik angegeben, so wird Butterworth als Default benutzt.
Filter mit Butterworth Charakteristik sind auf einen möglichst glatten Frequenzverlauf im Durchlassbereich ausgelegt. Bei der Grenzfrequenz haben sie eine Dämpfung von ca. 3 dB, das entspricht einer Halbierung der Leistung des Frequenzanteils an dieser Stelle.
Filter mit Bessel Charakteristik sind auf eine möglichst konstante Gruppenlaufzeit im Durchlassbereich ausgelegt, was einem möglichst linearen Phasengang im Durchlassbereich entspricht. Dadurch bleibt die Signalform des Eingangs-Signals nach der Filterung sehr gut erhalten. Die Dämpfung im Sperrbereich ist aber deutlich schwächer als bei Butterworth.
Filter mit Chebyshev Charakteristik sind auf ein möglichst scharfes Abknicken des Frequenzgangs bei der Grenzfrequenz, also eine möglichst schnelle Zunahme der Dämpfung im Sperrbereich nahe der Grenzfrequenz ausgelegt. Dafür ist der Frequenzgang im Durchlassbereich aber nicht mehr so glatt, sondern hat eine „Welligkeit“, d. h. die Frequenzanteile im Durchlassbereich werden je nach Frequenz ein wenig abgeschwächt oder verstärkt. Diese Welligkeit kann über einen Parameter im Bereich von 0.001 dB bis 1.0 dB eingestellt werden.
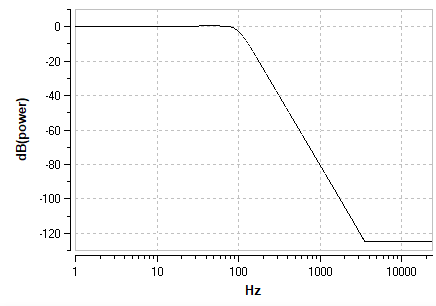
Zum Vergleich sind hier die Frequenzgänge der drei Filter- Charakteristiken grafisch dargestellt, jeweils für einen Tiefpass 4. Ordnung bei 100 Hz, bei einer Abtastrate von 48 kSPS.
Butterworth |
|
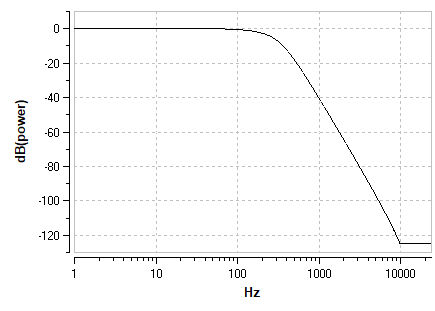
Bessel |
|
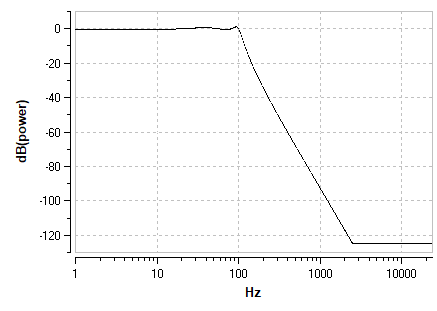
Chebyshev mit 1 dB Welligkeit im Durchlassbereich |
|
Die Berechnung eines Tiefpass-Filters erfolgt mit der Funktion ‚lowpass‘, die drei bis fünf Parameter haben kann, so dass der Aufruf dann wie in einer der drei nachfolgenden Zeilen aussieht:
lowpass ( data, edge, ord )
lowpass ( data, edge, ord, style )
lowpass ( data, edge, ord, style, ripple )
Und entsprechend auch für die Berechnung eines Hochpass-Filters:
highpass ( data, edge, ord )
highpass ( data, edge, ord, style )
highpass ( data, edge, ord, style, ripple )
Die Berechnung eines Bandpass-Filters erfolgt mit der Funktion „bandpass“, die vier bis sechs Parameter haben kann, so dass der Aufruf dann wie in einer der drei nachfolgenden Zeilen aussieht:
bandpass ( data, lower, upper, ord )
bandpass ( data, lower, upper, ord, style )
bandpass ( data, lower, upper, ord, style, ripple )
Und entsprechend auch für die Berechnung eines Bandstop-Filters mit der Funktion „bandstop“:
bandstop ( data, lower, upper, ord )
bandstop ( data, lower, upper, ord, style )
bandstop ( data, lower, upper, ord, style, ripple )
Dabei ist für den Parameter ‚data‘ der Name des Eingangs-Signals einzusetzen.
Für den Parameter ‚edge‘ bei „lowpass“ und „highpass“ ist die gewünschte Grenzfrequenz in Hz einzusetzen, im Bereich von 0 bis zur halben Abtastrate.
Für den Parameter ‚lower‘ bei „bandpass“ und „bandstop“ ist die gewünschte untere Grenzfrequenz in Hz einzusetzen, im Bereich von 0 bis zur halben Abtastrate. Ebenso auch bei ‚upper‘ die gewünschte obere Grenzfrequenz in Hz.
Der Wert von ‚upper‘ muss dabei größer als der von ‚lower‘ sein.
Für den Parameter ‚ord‘ ist die gewünschte Filter-Ordnung einzusetzen, im Bereich von 1 bis 10.
Der Parameter ‚style‘ kann die Werte 0, 1 oder 2 haben. Je nachdem wird der Filter wie folgt berechnet:
style = 0 mit Butterworth-Charakteristik
style = 1 mit Bessel-Charakteristik
style = 2 mit Chebyshev-Charakteristik
Fehlt der Parameter ‚style‘, so wird als Default-Wert style = 0 (Butterworth) angenommen.
Der Parameter ‚ripple‘ kann Werte von 0.001 bis 1.0 annehmen, wird aber nur bei Chebyshev-Charakteristik ausgewertet, und ansonsten ignoriert.
Fehlt der Parameter ‚ripple‘, so wird als Default-Wert ripple = 0.1 angenommen.
Die Parameter für die Grenzfrequenzen (edge, lower, upper) können sich während der Messung ändern, wenn ihnen eine entsprechende float Variable zugewiesen wird. Die anderenParameter werden am Start der Messung einmal ausgewertet, die Eigenschaften bleiben dann bis zum Ende der Messung unverändert. (Selbst wenn also z.B. eine float Variable als Ordnung ord angegeben wird und der Wert der Variable sich während der Messung ändert, bleibt die Ordnung für den Filter konstant).
Die Funktionen ‚lowpass‘, „highpass“, „bandpass“ und „bandstop“ liefern als Ergebnis ein Signal das genau wie das Eingangs-Signal weiter verarbeitet werden kann.